I recently visited the National Museums Collection Centre to study a rather remarkable artifact: a casing stone from a pyramid of Giza. The casing stones have a sloped, triangular face and formed the outer surfaces of the pyramids, as opposed to the inner blocks, which were left roughly hewn and were approximately cuboid. This stone was mined at the quarries in Tura on the east bank of the Nile 45 centuries ago, transported to Giza on the west bank, then carefully shaped with copper tools and placed in position on the outside of one of the Old Kingdom pyramids.

The original architectural position of this particular block remains a bit of a mystery as it was found in the mounds of debris on the north side Great Pyramid of Khufu by Waynman Dixon in 1872. Dixon was an English engineer who was carrying out investigative work at Giza for the Astronomer Royal for Scotland, Charles Piazzi Smyth. Smyth was interested in the dimensions of the Great Pyramid and the stone was brought back to Edinburgh for him. Using the slope of the face of a casing stone, it is possible to calculate the side slope of all of the pyramid’s faces.

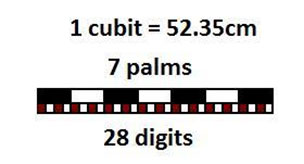
A full understanding of the dimensions of the pyramids and how they were established only came later, in part due to another discovery made by a Scottish archaeologist, Alexander Henry Rhind. The Rhind Mathematical Papyrus, now in the British Museum, contains many examples of arithmetical and geometric problems, including how to calculate the slope face of a pyramid. The ancient Egyptian methodology for defining a slope face began with the architects choosing the desired base and height dimensions for the pyramid, measured in Egyptian standard cubits. 1 cubit was a standard measurement length used all over ancient Egypt for measuring fields and constructing buildings. It was 52.35 cm long during the Old Kingdom when these pyramids were built, and this was broken down into 7 ‘palms’ of 4 ‘digits’ each.
Using straightforward arithmetic, the Rhind papyrus shows us how the side slope of the pyramid faces could be calculated from the chosen pyramid height and side length, and defined numerically by working out its ‘seked’. This seked is the name the Egyptians used for their slope system. It is a little like modern day degrees and angles, or inclines quoted in percents like we see on road signs for steep hills. According to the Rhind papyrus, the seked slope consisted of the number of palms moved across horizontally for each 1 cubit rise.

In order to understand the pyramids and this casing stone in Edinburgh then, we need to approach their study using these ancient Egyptian measurement systems.
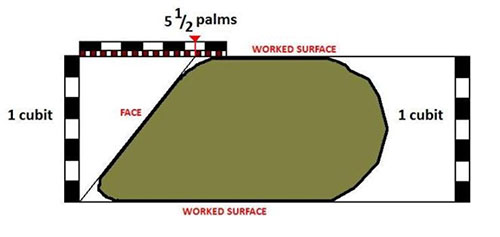
The block is only partially preserved, but the three all-important worked faces—the base, top, and sloped face—are mostly intact. Only a portion of the base survives though, so the block sits on its side, meaning I could not use an inclinometer to measure the slope. Nevertheless, tools can be used in different ways, and by placing the flat edge of a laser spirit level against the top face of the stone and holding an inclinometer’s pendulum at the known angle of the Great Pyramid against the stone’s face, it confirmed the correct angle known for the Great Pyramid of 51.84 degrees. Note that the accuracy of this measurement is only around 1 degree at best, and so it was carried out only to verify the known data rather than to establish new data.

After this was done, I brought out replica ancient Egyptian cubits rods. On one of them I had already marked off 5 1/2 palms, which is the known seked of the Great Pyramid. When used with another cubit, the two formed a triangle with a seked slope face of 5 1/2. By placing the marked cubit against the top surface I could then use the second cubit as a vertical to check the size of the slope using the cubits. In this case the second cubit should touch the face surface at some point allowing a measurement. The erosion of the lower corner of the block had rounded off that edge, so I placed a flat plank against the bottom of the stone. I was surprised to see that the darker cubit rod fit exactly between the upper white cubit and the plank, indicating that the casing stone was exactly 1 cubit thick.

That experiment alone shows how much information can be derived from artefacts themselves. Though it is essentially a large chunk of limestone, the block revealed significant information about the cultural and technical systems of the ancient Egyptians. But this particular angle or seked also has a more profound geometric significance, which is what makes this issue even more fascinating to study:
A pyramid with a face angle of 51.84 degrees has a base perimeter equal to a circle formed by its vertical height
Smyth thought that this was deliberate, but he drew a series of unfounded conclusions about the significance of this geometric relationship. The great Egyptologist Flinders Petrie followed Smyth’s work with a more scientific study and detailed triangulation survey of the whole Giza Plateau in 1882.
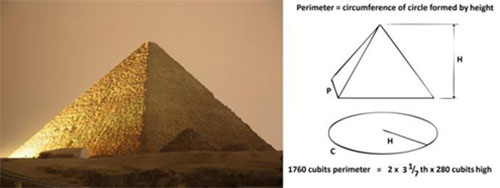
Petrie was certain that the circular symbolism had been intentional and wrote “…these relations of areas and of circular ratio are so systematic that we should grant that they were in the builder’s design”. He also found the same proportions and related numerical dimensions used in the construction of the king’s burial chamber in the Great Pyramid, and in other pyramids as well. My own contribution to this subject was to check all of the data again, and try and identify what this symbolic architectural choice meant to the ancient Egyptians within their own cultural systems of thought. The special proportions were likely a manifestation of a deep-seated belief in the power of encircling protective symbolism. The most notable expression of this concept is the shen ring, which was often shown carried above the pharaoh by the royal patron god Horus, the falcon, from as early as the Third Dynasty.
The clearest textual manifestation of this symbolism with respect to the pyramids is undoubtedly Pyramid Text 534, a ‘spell of protection’ for the pyramid:
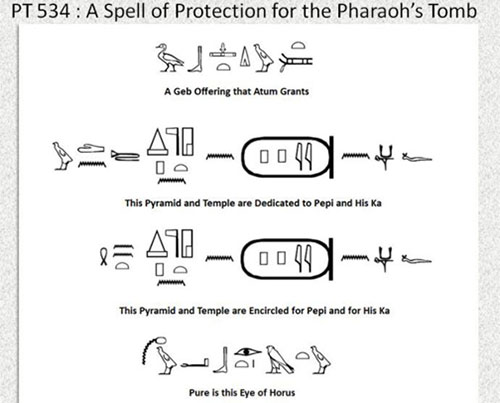
This spell or prayer of protection is written on the walls of the entrance passage into the pyramid of Pepi I at south Saqqara and may describe the rituals involved with building this monument. The text starts with a ‘Geb offering’, which may allude to a foundation deposit made at the start of the construction as Geb is the god of the earth. This is followed by lines describing how the pyramid and temple are then ‘established’ and then ‘encircled’ to make them pure; an ‘eye of Horus’. The encircling here, using the word shen, implies that the pyramid is also protected by this action.

One final mystery remains, however. Heavy though this casing stone is, it is small compared to the giant sloped stones still in place along the northern side of the base of the Great Pyramid. It is possible the Edinburgh block might come from one of the similarly proportioned Queens’ pyramids, built at the same time as the Great Pyramid, but with smaller casing blocks. However, it might more likely come from the upper levels of the Great Pyramid, near the peak. As Mark Lehner described for the second pyramid of Khafre, which still has some casing stones in place, ‘the casing stones at the top of the pyramid are much smaller – about 1 cubit thick (c. 50cm/20 in)’. The Edinburgh casing stone, therefore, is most likely to be a rare survival from the summit of Khufu’s extraordinary pyramid, 146 meters high when completed. This stone, however, is not ‘approximately’ 1 cubit tall, it seems to be precisely 1 cubit tall. This level of precision would fit with what we know of the Great Pyramid, for which the standards of workmanship and consistency were greater than for many, if not all, of the later pyramids. This unadorned block of broken stone has remarkable historical and scientific significance, both regarding the ancient world and the 19th century world, and continues to reveal new information.
Thanks to Margaret Maitland, Curator of the Ancient Mediterranean at National Museums Scotland, and Alan Jeffreys of Egyptology Scotland for help in this research project.
You can read the full version of this post here.
